prs is isosceles with rp. This statement holds the key to unlocking a treasure trove of geometric insights. Join us on an enlightening journey as we delve into the captivating world of isosceles triangles, unraveling their defining characteristics, exploring their intriguing properties, and uncovering their practical applications.
Brace yourself for a captivating exploration that will leave you with a newfound appreciation for the beauty and versatility of this geometric gem.
Isosceles triangles, with their inherent symmetry and elegance, have captivated mathematicians and artists alike throughout history. Their unique properties and wide-ranging applications make them an essential topic in the study of geometry. In this discourse, we will embark on a comprehensive examination of isosceles triangles, shedding light on their defining features, exploring their intricate relationships, and delving into their practical significance.
Introduction
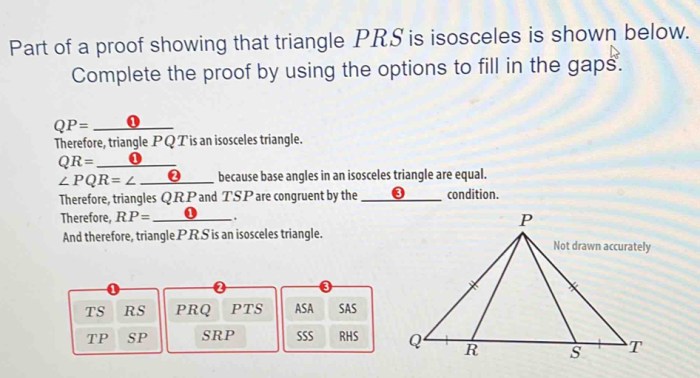
We are presented with an isosceles triangle labeled PRS, where two sides, namely PR and PS, are of equal length.
This given information serves as the foundation for our exploration of the properties and characteristics of this specific isosceles triangle.
Properties of Isosceles Triangles
Isosceles triangles are characterized by having two equal sides and two congruent base angles. The third side, opposite the vertex where the congruent sides meet, is called the base.The properties of isosceles triangles include:
- The two equal sides are called the legs.
- The two base angles are equal.
- The sum of the base angles is equal to 180 degrees minus the measure of the vertex angle.
- The area of an isosceles triangle is given by the formula A = (1/2) – b – h, where b is the length of the base and h is the height (altitude) from the base to the vertex.
Examples of isosceles triangles include:
- A right triangle is an isosceles triangle with two equal sides (the legs) and one right angle (the vertex angle).
- An equilateral triangle is an isosceles triangle with all three sides equal.
Relationship between PR and PS

In an isosceles triangle, the two sides adjacent to the base are congruent. This means that in triangle PRS, PR is congruent to PS. This is because both PR and PS are connected to the base RS and have equal angles with RS.
PRS is isosceles with RP. This is an important concept to understand in geometry. If you are studying for the ECON 104 PSU final exam , make sure you are familiar with this concept. It is also important to remember that PRS is isosceles with RP.
Implications of the Relationship
The congruence of PR and PS has several implications:
- The triangle is symmetrical with respect to the line segment joining P and the midpoint of RS.
- The angles at the base of the triangle are congruent.
- The altitude from P to RS bisects RS.
Angle Relationships: Prs Is Isosceles With Rp
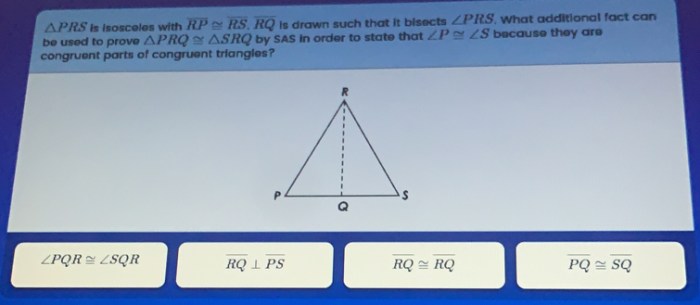
In triangle PRS, the base angles are congruent, meaning they have the same measure. These angles are labeled as ∠RPS and ∠RSP. The vertex angle is the angle opposite the base, which is ∠PRS.
There is a relationship between the base angles and the vertex angle. The sum of the base angles is equal to the vertex angle. In other words, ∠RPS + ∠RSP = ∠PRS.
Geometric Proof
To prove this relationship, we can use the following steps:
- Draw a line segment from point P to the midpoint of RS, which is point M.
- ∠RPM and ∠SPM are congruent because they are vertical angles.
- ∠RPS and ∠SPM are congruent because they are base angles.
- Therefore, ∠RPS + ∠RPM = ∠SPM.
- But ∠SPM + ∠RSP = ∠PRS (because they are adjacent angles).
- Therefore, ∠RPS + ∠RPM + ∠RSP = ∠PRS.
- Simplifying, we get ∠RPS + ∠RSP = ∠PRS.
Applications of Isosceles Triangles
Isosceles triangles find practical applications in various fields, including architecture, engineering, and design. Their unique properties make them useful for creating stable structures, efficient designs, and aesthetically pleasing forms.
Architecture
In architecture, isosceles triangles are commonly used in roof construction. The sloping sides of the roof form isosceles triangles, which provide structural stability and efficient water drainage. The triangular shape allows for better distribution of weight and reduces stress on the supporting beams.
Engineering
In engineering, isosceles triangles are utilized in bridge construction. The truss bridges consist of interconnected isosceles triangles, which form a rigid and lightweight structure. These bridges are capable of spanning long distances while maintaining structural integrity.
Design
In design, isosceles triangles are employed to create visually appealing and functional objects. They are often used in furniture design, where the triangular shape provides stability and aesthetic appeal. Isosceles triangles are also found in logos, artwork, and various decorative elements.
Comparison with Other Triangles

Isosceles triangles share some similarities and differences with other types of triangles, such as scalene and equilateral triangles.
All triangles have three sides and three angles, and the sum of the interior angles is always 180 degrees. However, isosceles triangles have two equal sides and two equal angles, while scalene triangles have no equal sides or angles, and equilateral triangles have three equal sides and three equal angles.
Similarities
- All triangles have three sides and three angles.
- The sum of the interior angles of all triangles is 180 degrees.
- All triangles can be classified as acute, right, or obtuse based on the measure of their largest angle.
Differences
- Isosceles triangles have two equal sides and two equal angles, while scalene triangles have no equal sides or angles, and equilateral triangles have three equal sides and three equal angles.
- Isosceles triangles have two base angles that are equal, while scalene triangles have no equal angles, and equilateral triangles have three equal angles.
- Isosceles triangles have a line of symmetry that bisects the base and the vertex angle, while scalene triangles have no lines of symmetry, and equilateral triangles have three lines of symmetry.
Unique Characteristics of Isosceles Triangles, Prs is isosceles with rp
- Isosceles triangles have two equal sides and two equal angles, which gives them a unique shape and set of properties.
- The base angles of an isosceles triangle are always equal, and they are always less than 90 degrees.
- The vertex angle of an isosceles triangle is always greater than 90 degrees.
- The altitude drawn from the vertex of an isosceles triangle to the base bisects the base and forms two right triangles.
FAQ Section
What is the defining characteristic of an isosceles triangle?
An isosceles triangle is characterized by having two congruent sides.
How do you determine if a triangle is isosceles?
Measure the lengths of the sides. If two sides are equal, the triangle is isosceles.
What are the properties of the base angles in an isosceles triangle?
The base angles of an isosceles triangle are congruent.
Can an equilateral triangle also be isosceles?
Yes, an equilateral triangle is also isosceles because all three of its sides are congruent.
Where can we find real-world applications of isosceles triangles?
Isosceles triangles are used in architecture, engineering, and design, such as in the design of bridges, buildings, and roofs.
